
Fibonacci
Adding up second terms together, 2 (N1) = (N1) X X = {1 2 3 (N2) (N1) N} { (N) (N1) (N2) 3 2 1} I hope it's clear by now that every combination adds up to (N1), and there are N such combinations (N terms in the summation whic Continue Reading Related Answer Daniel Kim , I ate pi last week= 1 Where is Factorial Used?
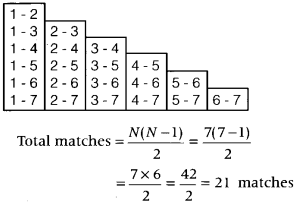
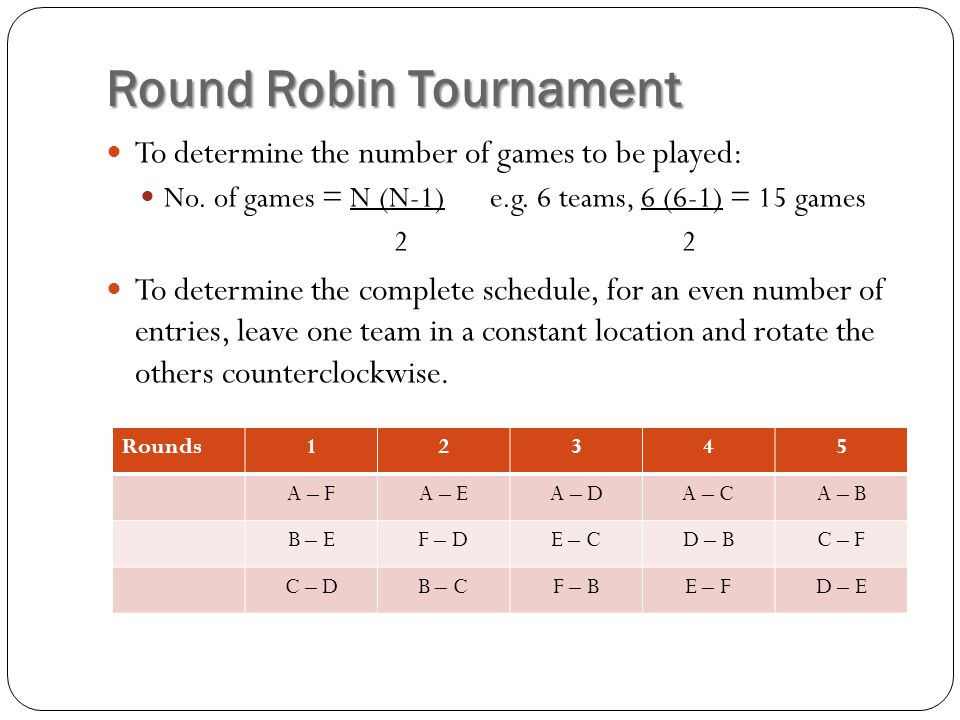
N(n-1)/2 formula is used in tournaments)
N(n-1)/2 formula is used in tournaments)- Transcript Prove 1 2 3 n = (n(n1))/2 for n, n is a natural number Step 1 Let P(n) (the given statement)\ Let P(n) 1 2 3 n = (n(n1))/2 Step (N1) (N2) 2 1is a sum of N1 items Now reorder the items so, that after the first comes the last, then the second, then the second to last, ie (N1) 1 (N2) 2 The way the items are ordered now you can see that each of those pairs is equal to
Solved For Each Positive Integer N Let P N Be The Sentence In Any Round Robin Tournament Involving
4 Applying other theorems about behavior of limits under arithmetic operations with sequences, we conclude that lim 1 2 q 1 1 4n 2 = 1 2·12 = 1 4 95 Let t1 = 1 and tn1 = (t2 n 2)/2tn for n ≥ 1 Assume that tn converges and find the limitNow how many ways can we arrange no letters?We can use the formula to find the nth term of the sequence, where n n is any positive number In our example, each number in the sequence is double the previous number, so we can use powers of 2 to write a formula for the n th n th term The first term of the sequence is 2 1 = 2, 2 1 = 2, the second term is 2 2 = 4, 2 2 = 4, the third term is 2 3 = 8, 2 3 = 8, and so on The n th n th term of
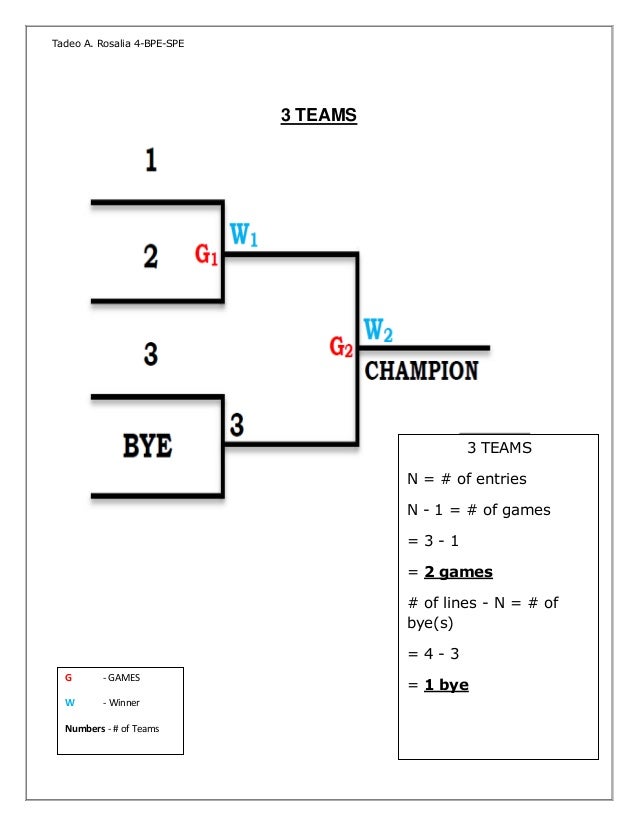
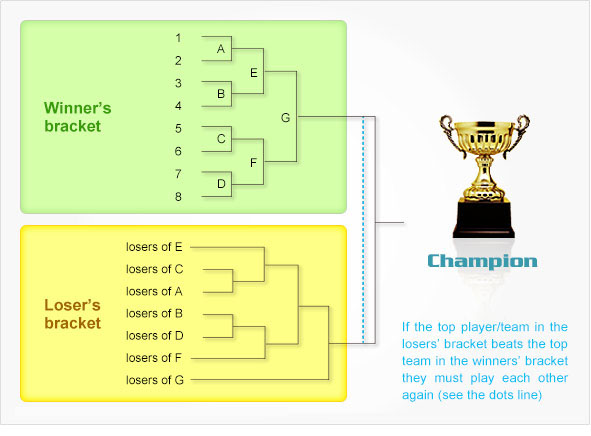
Answer a n = a n1 3%a n1 = 103 * a n1, where a n is the population of the world n years after 1995, and a 0 is the population of the world in 1995, which is 7 billion b) Find an exiplicit formula for the population of the world n years after 1995 Here, all the teams play with all teams Suppose if there are n no of teams playing a tournament, then the "first team plays" with n1 teams, the "second team plays" with n2 teams and so on Hence, by mathematical induction, the no of matches played is the total of (n1) (n2) 1 So, the total no of games is equal to Advertisement Answer Single League Number of matches \(=\frac { N(N1) }{ 2 }\) (N = Number of teams) Double League Number of matches = N (N1) (N = Number of teams) Fixture Any tournament whether it is knockout or league, is arranged according to a set procedure which is known as fixture For knockout tournament, the procedure to draw fixture is through bye and seeding
N(n-1)/2 formula is used in tournaments)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
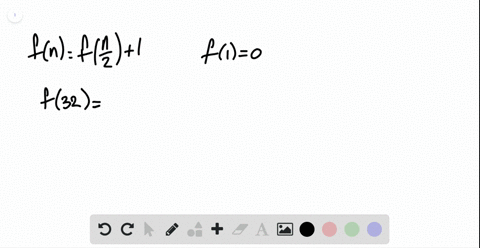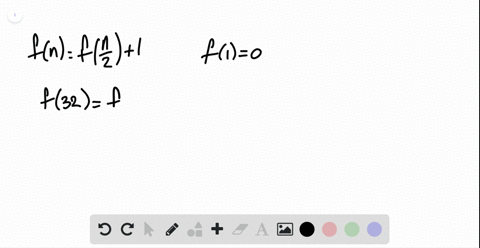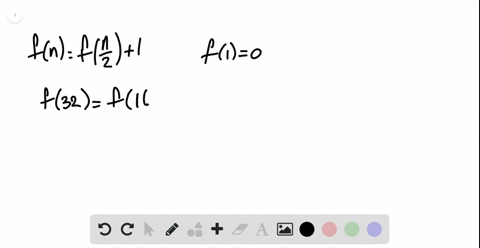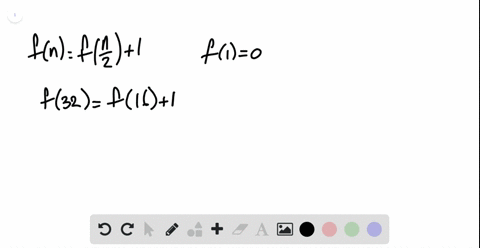 |  | |
 |  | |
 | ||
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 | ||
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
/pic3075594.png) |  |  |
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「N(n-1)/2 formula is used in tournaments)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
RS n =arar 2 ar 3 ar n1 ar n 2 Subtracting Equation 2 from Equation 1, we get (1r)S n =aar n So, the sum of n terms of a geometric series with starting value a, ratio, r is Probably because of the financial (compound interest) applications of the geometric progression, the formula is written assuming that r is less than one, but if r is greater than 1, then the minusesOne area they are used is in Combinations and Permutations We had an example above, and here is a slightly different example Example How many different ways can 7 people come 1 st, 2 nd and 3 rd?





0 件のコメント:
コメントを投稿